数学建模笔记

题目类型:

• 优化
• 机理分析
• 预测
• 评价

重点:

• 常用算法
• 常用模型
• Matlab 算法编写
• Omnigraffle
• LaTeX
• Lingo
• 微分方程的应用
• 图论算法
• 离散化问题
• 评价类 => SPSS

常用模型

线性规划

目标函数 决策变量
线性约束条件

约束条件区间不连续 => 分段 分成多个子问题

可加入松弛变量 表示剩余量

可用变量替换将一般问题转化为线性规划

可通过简化将多个目标函数中的某些个转化为约束条件 或适当忽略

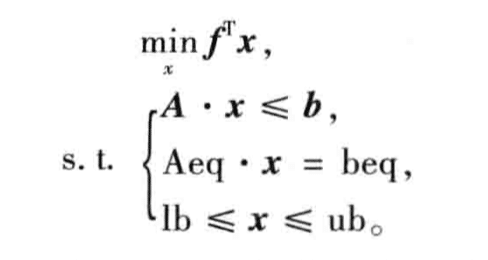
f = [f1; f2; ...];
a = [_, _, ... ; ...; ...]; b = [_, _, ... ; ...; ...];  % 矩阵各行用 ; 分开
aeq = [_, _, ...];
beq = _ ;
lb = _;
ub = _;
[x, fval] = linprog(f, A, b, Aeq, beq, lb, ub)

x 返回决策变量的取值，fval 返回目标函数最优值

没有对应约束时，对应矩阵为空矩阵，用 [ ] 表示

场景

• 投资 收益 & 风险
• 加工场景 原料费 销售额 & 利润

插值 & 拟合

主要用于预测类模型

生成一些新的但又比较靠谱的值，从而更好的数据分析，进一步确定模型

也可选用 cftool

一维插值

y = interp1(x0, y0, x, 'method')
% method: 
% nearest 最近项
% linear 线性
% spline 三次样条
% cubic 立方

分段三次埃尔米特插值

直接使用埃尔米特插值得到的多项式次数较高，存在龙格现象，产生波动，所以用分段三次埃尔米特插值

x = -5:5;
y = [1 1 1 1 0 0 1 2 2 2 2];
p = pchip(x,y);
xq = -5:0.2:5;
pp = ppval(p,xq);  % 返回插值函数的查询点处的y坐标

三次样条插值

format long g
t0 = 0.15:0.01:0.18;
v0 = [3.5 1.5 2.5 2.8];
pp = csape(t0,v0)    % 三次样条插值函数
xishu = pp.coefs;    % 三次样条插值函数的系数
s1 = integral(@(t)fnval(pp,t),0.15,0.18);   % 求积分(离散点数值积分)
format          % 恢复短小数据形式

二维插值

interp2(x0,y0,z0,x,y,'method');

% 三次样条
pp = csape({x, y}, z);
z = fnval(pp, {x, y});

% 对于散乱节点(xi, yi, zi)
ZI = griddata(x, y, z, XI, YI, 'method');

zi1 = griddata(x,y,z,xi,yi','cubic');  % 立方插值
zi2 = griddata(x,y,z,xi,yi','nearest');  % 最近点插值
zi = zi1;  % 立方插值和最近点插值的混合插值的初始值
zi(isnan(zi1)) = zi2(isnan(zi1))  % 把立方插值中的不确定值换成最近点插值的结果
% isnan(zi) 返回一个和 zi 同大小矩阵，并将 zi 中的 NaN 替换为1，其他替换为0
% zi(isnan(zi1)) 返回一个 m*1 矩阵，值均为 zi 中对应位置的值 NaN
% 外插值不确定 => 混合插值

拟合——线性最小二乘法

最小二乘原则: 拟合的y与原f(x)距离的平方和最小

可先观察数据进行分段后再处理

可先通过图像大致判断，再用多种曲线拟合&比较

% 已知多项式 y = a + bx^2
r = [ones(5,1),x.^2];  % 行数和数据数量对应
ab = r\y;
x0 = 19:0.1:44;
y0 = ab(1) + ab(2) * x0.^2;
plot(x,y,'o',x0,y0,'r');

a = polyfit(x0, y0, m)  % m为多项式次数
y = ployval(a, x);  % 计算y

最小二乘优化

目标函数为平方和

Matlab 中的 lsqlin, lsqcurvefit, lsqnonlin, lsqnonneg 4个函数可选

曲线逼近

最小平方逼近

正交多项式

场景

• 离散的检测数据处理
• 估计任意…的方法

整数规划

整数 线性规划

匈牙利算法

蒙特卡洛

% 与线性规划类似
x=intlinprog(c,intcon,[],[],a,b,lb,ub);  % intcon为变量个数

用Lingo 可以避免自己转化约束条件和变量变换 避免将多维变量转化为一维变量

0-1规划

可将相互排斥的约束条件化为0-1变量的形式 加在约束条件内 形成一个更综合的约束条件

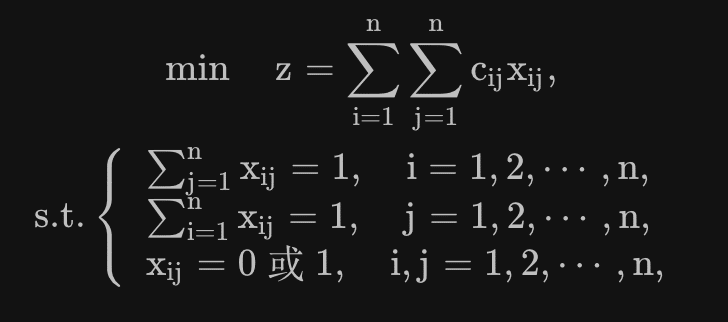
场景

• 指派
• 0-1背包
• 二选一

非线性规划

若有0-1决策变量xi 满足 xi(1-xi) = 0

[x, fval] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, options)
% fun 目标函数
% nonlcon 是用m文件定义的非线性向量函数 分为非线性不等式约束 & 非线性等式约束
% nonlcon 写法: function [g, h] = fun_name(x) => g表示不等式 h表示等式 每个条件换行 []

和线性规划不同，非线性规划求出来的是局部最优解
所以起始点 x0 的选取很重要:

1. 多个初始值
2. 蒙特卡洛模拟出一个值 将这个值作为初始值
3. 还可以尝试多个 option 如 interior-point, sqp, active-set, trust-region-reflective 多种算法 可在计算中对比

无约束时，fminunc & fminsearch
fminunc 算法更好一点 用导数

二次规划

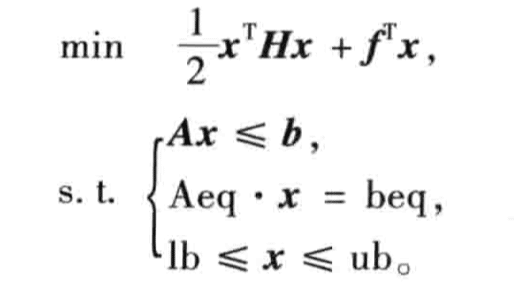
% 二次规划
[x, fval] = quadprog(H, f, A, b, Aeq, beq, lb, ub, x0)
% H为二次项系数矩阵，x1,x2...之间用;隔开，变量依次由高次到低次系数*2

罚函数法

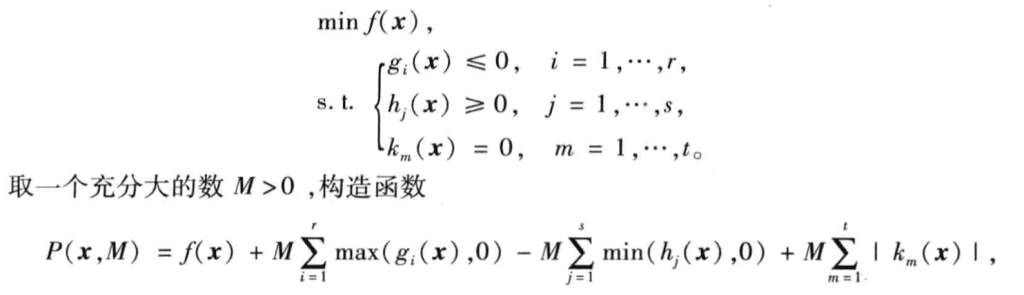
写m函数 直接用fminunc就可

场景

• 多个条件
• 较为简单的目标

目标规划

多目标决策问题

绝对约束 => 严格相等
目标约束 => 允许偏差

正偏差变量 负偏差变量

优先因子
权系数
这两个 => 查文献 or 不行就自己考虑决定

目标函数

恰好 => 正偏差变量和负偏差变量 min
不超过 => 正偏差变量 min
超过 => 负偏差变量 min

模型表示

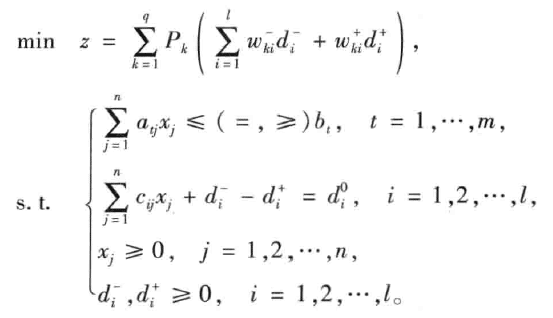
第一个条件为绝对约束 不用动
第二个为目标约束 将不等式转为等式
之后是变量范围

matlab 实现

[x, fval] = fgoalattain('fun', x0, goal, weight, A, b, Aeq, beq, lb, ub, nonlcon)

% 实例
[x1,g1]=linprog(c1,a,b,[],[],zeros(4,1))  %求第一个目标函数的目标值
[x2,g2]=linprog(c2,a,b,[],[],zeros(4,1))  %求第二个目标函数的目标值
g3=[g1;g2];  %目标goal的值
[x,fval]=fgoalattain(fun,rand(4,1),g3,abs(g3),a,b,[],[],zeros(4,1))

算法

场景

• 尽量 or 尽可能 满足什么条件

动态规划

多阶段优化

每次决策依赖于当前状态，又随即引起状态的转移。
一个决策序列就是在变化的状态中产生出来的

动态规划的优势是记住求过的解来节省时间

条件

• 最优解原理
• 无负反馈
• 每个子问题不独立

过程

1. 划分阶段 要有序
2. 确定状态变量
3. 确定决策并写出状态转移方程 递推关系
4. 临界条件

最短路

Dijkstra算法 Floyd算法

% 定义路线权值 w
w = [2 1 8 6 1 7 9 5 1 2 3 9 4 6 3];

% 邻接矩阵的构造
% sparse 构建稀疏矩阵

% sparse(i,j,v,m,n) 将 S 的大小指定为 m×n
% i和j各位置一一对应 每个位置代表一条路径 w对应位置的数字为该路径的权值
% 第i行第j列表示从i节点到j节点
% 其余位置为0
DG = sparse([1 1 1 2 2 3 3 4 4 4 5 5 6 6 7],[2 3 4 4 5 4 7 5 6 7 6 8 7 8 8],w,8,8);

first = input('请输入初始节点：');
last = input('请输入终止节点：');

% 用 graphshortestpath 求解
[dist,path,pred] = graphshortestpath(DG,first,last);

% 有向赋权图的绘制
h = view(biograph(DG,[],'ShowWeights','on'));

% 标记路线经过的节点
set(h.Nodes(path),'Color',[1 0.6 0.6]);  % []中三个数字代表 RGB

% 标记路线经过的路径
edges = getedgesbynodeid(h,get(h.Nodes(path),'ID'),get(h.Nodes(path),'ID'));
set(edges,'LineColor',[1 0 0]);
set(edges,'LineWidth',2.0);

回归分析

因果

相关性分析

散点图

spss 导入数据 相关分析

相关系数计算

线性回归

随机误差项

分析涉及:

• 参数估计
• 方差估计
• 显著性检验

最小二乘法

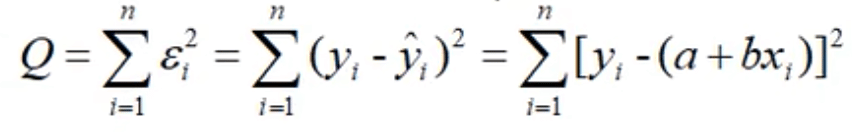
残差平方和 => 最小值 => 关于参数求偏导=0 => 得到bhat

假设检验

判定系数 => x之间相关程度
复相关系数R

偏最小二乘回归分析

多个因素中的两个之间关系分析

回归函数的估计

matlab 实现

% 一元线性回归
b = regress(y,X)
[b,bint] = regress(y,X)
[b,bint,r] = regress(y,X)
[b,bint,r,rint] = regress(y,X)
[b,bint,r,rint,stats] = regress(y,X)
[___] = regress(y,X,alpha)

% B：回归系数，是个向量（“the vector B of regression coefficients in the  linear model Y = X*B”）
% BINT：回归系数的区间估计（“a matrix BINT of 95% confidence intervals for B”）
% R：残差（ “a vector R of residuals”）
% RINT：置信区间（“a matrix RINT of intervals that can be used to diagnose outliers”）
% STATS：用于检验回归模型的统计量。有4个数值：判定系数R^2，F统计量观测值，检验的p的值，误差方差的估计q
% ALPHA：显著性水平（缺少时为默认值0.05）

聚类

k-means 聚类

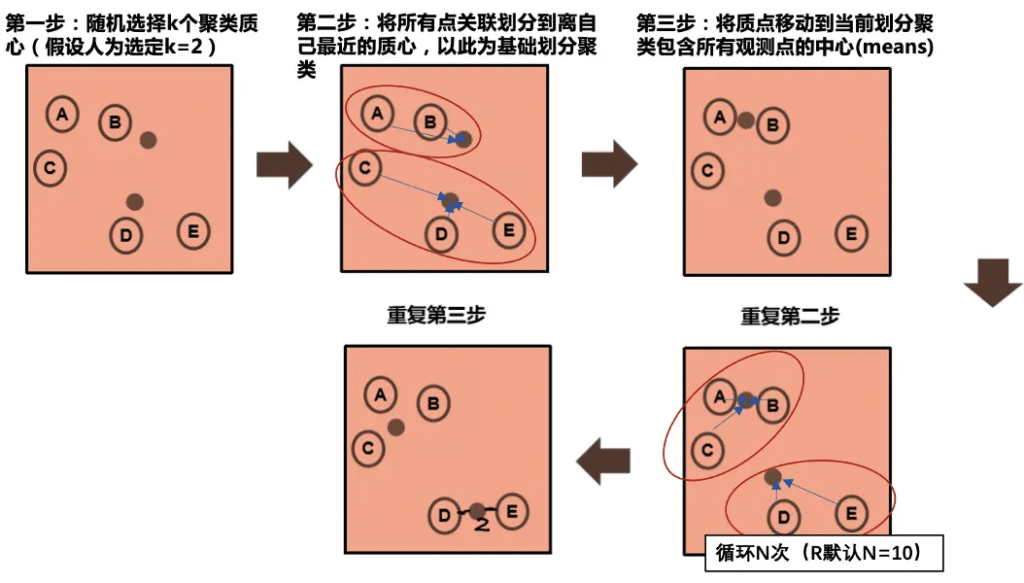
先处理数据，归一化等，再随机选择k个聚类质心，随后参照质心划分数据点，以此划分基础聚类。将每个聚类的质心移到聚类所包含的数据点的中心。

重复上述操作，直到所有点到其所属聚类质心的距离平方和最小 (发生突变)

容易产生局部最优 => 通过多次随机来解决

k-means 质心选择

• 肘部法则 => 横轴为K的取值，纵轴为距离平方和定义的损失函数 => 找拐点
• 拍脑袋法
• gap statistic法 => 通过蒙特卡洛模拟产生logDk的期望E(logDk)，在区域内均匀分布随机产生和原始样本数一样多的随机样本，做k-means，得到对应的损失函数Dk，重复多次得出E(logDk)的近似值，从而最终可以计算gap statistic => 找gap statistic最大值对应的K

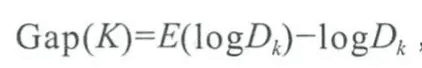
• 轮廓系数

场景

• 求差异
• 划分类别

优化类算法讨论

1. 找关键变量
2. 找关系 & 方程
3. 把已知式子转化为模型

凸函数

梯度下降效率高

非凸函数

• 粒子群算法 => 抉择变量连续 => 连续收敛速度快，但跳出局部最优解能力较弱
• 遗传算法 => 抉择变量离散 => 收敛速度慢，但跳出局部最优解能力强
• 模拟退火 => 收敛速度快且跳出局部最优解能力强，但不好处理多维决策变量

数据分析类总结

数据处理

可以用 SPSS 进行很多统计学上的套路分析，导入数据后有现成的工具，不用编程。

数据获取

国家统计局，国外的统计平台，开放平台，爬虫爬取网页页面上的数据

数据清洗

• 删去异常值
• 离散 vs. 序列 => 如何处理看具体情景
• 插值扩充
• 正态分布检验

初步处理

1. 可视化 => 波动？周期？特征？
2. 数值运算 => 求导？差分？
3. 标准化 => 极差，均方差等
4. 简单拟合
5. 分类分析 => 聚类分析
6. 相关性分析
7. 降维 => 主成分分析，因子分析
8. 量化分析

模型搭建

• 参数拟合 => 线性？ 最小二乘 梯度下降…
• 预测 => 时序 => fbprophet, arima, 指数平滑, 拟合后处理, GM11…
  or 空间 => 抽象图，网格化(莫兰指数, 元胞自动机, 自定义空间演化)
• 对于离散的数据，使用量化(ABC对Y的影响，关系；评价类) => 多元非线性拟合
  1. 优先看能不能转化为线性
  2. 画图看
  3. 通过文献确定权重等等
  4. 综合评价 => AHP, FAHP, 模糊综合评价, 灰色关联分析 => 确定权重
• 半监督模型 => BP, 支持向量机

模型改进

一定要创新，至少要改些小地方，可交叉使用 or 缝合怪

检验

• 交叉检验
• “评价“评价算法
• 算法检验 => 鲁棒性，灵敏性，泛化能力
  过拟合检验？

评价算法的评价 & 检验

• 多种模型对比
• 结合实际情况分析 => 多写多阐释

Matlab 常用语法

计算 & 求值

最值

xmm=minmax(x)  % xmm = [xmin, xmax], xmin = xmm(1), xmax = xmm(2)
ymm=minmax(y)  % ymm = [ymin, ymax], ymin = ymm(1), ymax = ymm(2)

定积分

integral(f, a, b)
% a => 积分下限
% b => 积分上限
% f 可为匿名函数

随机生成

randi([0,99],1,5);  % 产生一行五列的区间[0, 99]上的随机整数
unifrnd(0,12,[1,100]);  % 随机生成1行100列 [0, 12]上的double

矩阵操作

[ , , , ...]'  % 转置
A\B = B/A
A(:,m)  % 获取矩阵A的第m列 返回列向量
A(:)  % 将矩阵压缩为一列
zeros(a, b)
ones(a, b)

画图

二维图像 & 图例

% plot函数 可有多组(多个图像) 其中第三个参数option 按内容分为改变坐标点or曲线样式
plot(X, Y)
plot(x, y, 'o', xq1, p, '-', xq1, s, '-.')

% 每个值对应 plot 中的一组(一条曲线) 对应生成图例
legend('Sample Points','pchip','spline','Location','SouthEast')

三维

mesh(X, Y, Z)

限定区间

ylim([ymin ymax])
xlim([xmin xmax])

多图共存

默认为 hold off 状态，新绘制的图替换掉旧图
在段落间使用 hold on 与 hold off 切换”是否覆盖”的状态

函数

文件定义函数

函数名与文件名完全一样

% function[输出形参表: output1, ...,outptn] = 函数名(输入形参表: input1, ... , inputn)
% e.g.
function [max,min] = max_min_values(X)
% ...
end

A = [1, 12, 13443, 134];
[m,n]=max_min_values(A);

匿名函数

% 匿名函数用法 @(variable)
sqr = @(n) n.^2;
x = sqr(3)

% "选择"
C = {@sin, @cos, @tan};
C{2}(pi) => ans = -1

S.a = @sin;  S.b = @cos;  S.c = @tan;
S.a(pi/2) => ans = 1

Ending

感觉就是东西真的太多了，肯定是不可能记的，大概也就是看完一个点到时候能记起来有这个东西就不错了，若是还能保证大部分内容的理解，赛前的准备也就达到目的了。

在准备的时候花时间写这篇博客，一是想在看的时候集中注意力，时刻要知道自己在看什么而不是走马观花，二是比赛的时候如果遇到看过的内容，就能来看看这篇博客能避免再浪费时间去查，这也算是一个记录，只能说内容确实比较流水，但如果真能发挥作用也就很好了。

GOOD LUCK

2022.9.13 国赛前两天 终