树 & 二叉树

概念

• 树 子树
• 结点
• 结点的度
• 树的度
• 叶子 (终端结点)
• 非终端节点
• 双亲 孩子
• 兄弟
• 祖先
• 子孙
• 层次
• 堂兄弟
• 深度 高度
• 有序树 无序树
• 森林

二叉树

• 可递归
• 至多两棵子树
• 有序
• 第 i 层至多 $2^{i-1}$ 个结点
• 深度 k 至多 2^k – 1 个结点
• 终端结点 $n_0$，度为2的结点 $n_2 则 n_0 = n_2 + 1$
• 满二叉树
• 完全二叉树
• 具有 n 个结点的完全二叉树深度为 $\log_2 n + 1$

存储结构

• 顺式浪费空间 ⇒ 链式
• TElemType data; struct BiTNode *lchild, *rchild;
• 图中 \wedge 表示空

遍历

• 线性化
  • 先序 ⇒ 根左右
  • 中序 ⇒ 左根右
  • 后序 ⇒ 左右根
• 算法
  • 递归
  • 非递归(栈)

根据遍历序列确定二叉树

先+中序 or 后+中序 中序序列是以根节点分隔左右 先序第一个节点 or 后序最后一个节点 为根节点，再次分隔，不断循环

算法 code here！！！

线索二叉树

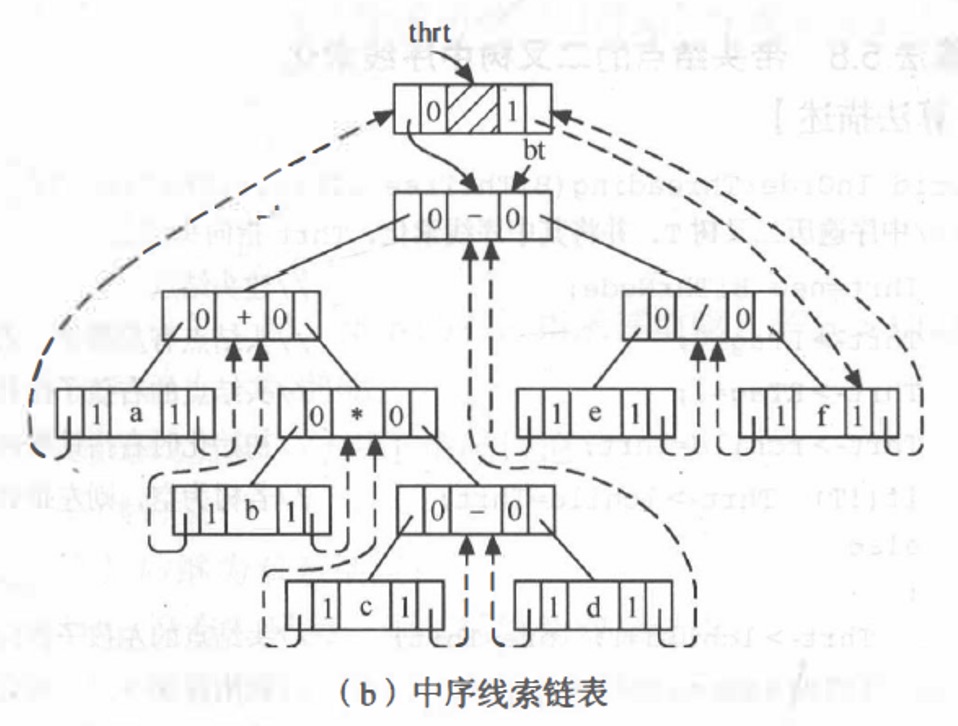
• lchild, LTag, data, RTag, rchild
• TElemType data; struct BiThrNode *lchild, *rchild; int LTag, RTag;
• LTag
  • 0 ⇒ lchild 指示左孩子
  • 1 ⇒ lchild 指示前驱
• RTag
  • 0 ⇒ lchild 指示右孩子
  • 1 ⇒ child 指示后继
• 线索链表 线索二叉树 线索化
• “双向线索链表”
• 先 中 后 序

树

• 可递归
• 可表示分等级的层次结构

存储结构

• 双亲表示法

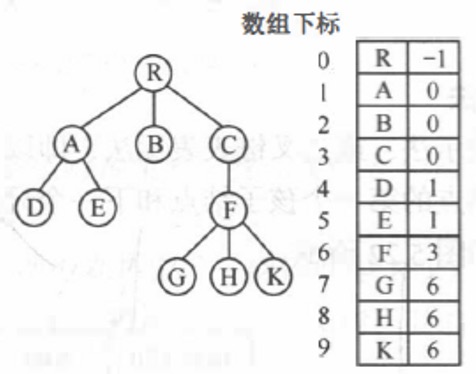
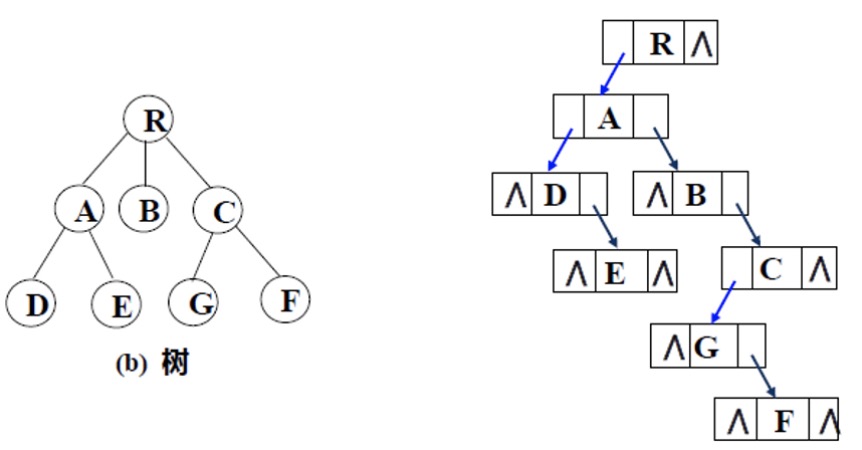
• 孩子表示法
• 孩子兄弟法

遍历

• 先序遍历 根 → 各子树依次先序
• 中序遍历 左 右 根
• 后序遍历 各子树依次后序 → 根

哈夫曼树

二叉树 每次选最小的两个作为叶子 求和后 重复这个过程

编码

左0 右1

Tips

• 节点个数 = 所有节点度数之和+1
• 创建二叉树时 一定要将树的节点指针作为返回值返回 不要只是传入然后进行修改 那样改的只是一个复制

程序实现

BiTree CreateTree(int index) {
   BiTree t;
   t = (BiTree)malloc(sizeof(BiTNode));
   t->data = a[index][2];
   if(a[index][0] == 0) {
       t->lchild = NULL;
  } else {
       t->lchild = CreateTree(a[index][0]-1);
  }
   if(a[index][1] == 0) {
       t->rchild = NULL;
  } else {
       t->rchild = CreateTree(a[index][1]-1);
  }
   return t;
}
​
void check(BiTree t) {
   if(t) {
       check(t->lchild);
​
       if(t->data < count) {
           count = -1;
           return;
      }
       count = t->data;
​
       check(t->rchild);
  }
}
​
void inOrderTraverse(BiTree t)
{
   if(t) {
       inOrderTraverse(t->lchild);
       printf("%d ",t->data);
       inOrderTraverse(t->rchild);
  }
}
int main() {
   BiTree t;
   scanf("%d", &n);
   for(int i = 0; i < n; ++i) {
       for (int j = 0; j < 3; ++j) {
           scanf("%d", &a[i][j]);
      }
  }
   t = CreateTree(0);
   check(t);
   if(count != -1) {
       printf("YES\n");
       inOrderTraverse(t);
  } else {
       printf("NO\n");
  }
}