定义
Kullback-Leibler Divergence (KL-divergence)
KL 散度 也称相对熵
衡量概率分布 P 对于概率分布 Q 的差异 ⇒ information difference
不是描述距离,无对称性
数学推导
熵 H —— 不确定程度
KL散度 (相对熵) —— 近似分布相对于原分布信息损失
$H = – sumlimits_{i=1}^N p(x_i) cdot log p(x_i)$
$D{KL}(p||q) = sumlimits{i=1}^N p(x_i) cdot cfrac{log p(x_i)} {log q(x_i)}$
在原来的概率分布p上加入近似的概率分布q,计算它们对数差的期望值
eg. 当取 $log_2$ 时,可以在实际中对应损失了多少 bit 的信息
实际用途
简化
在概率统计中可以用 KL 散度将实际问题中的复杂分布近似为简单的分布,即简化模型
优化
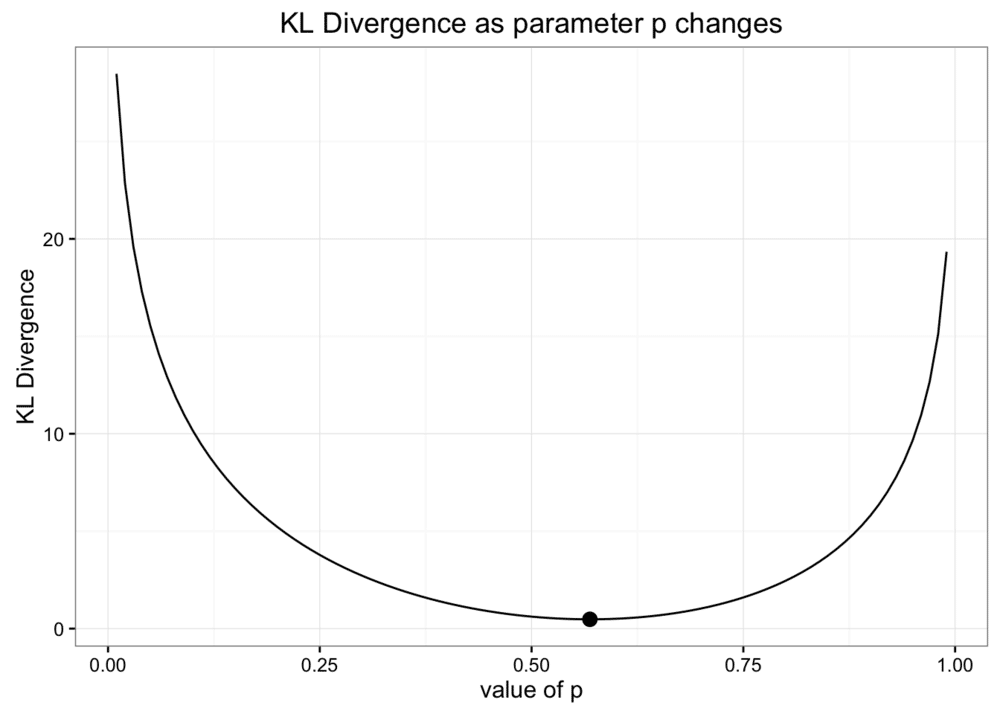
因为 KL 散度表示信息差,所以可以用 KL 散度作为指标调整参数进行优化,如下图,用 KL 散度调整二项分布中的参数p,获得最优参数
GAN
在 GAN 中使用经常使用 KL 散度来衡量生成器生成的样本与真实数据的接近程度,并以此训练
GAN 的生成器隐式地定义了一个概率分布,并依此概率分布来生成样本,所以 GAN 的训练目标是使生成器定义的隐式的概率分布,尽可能地接近训练样本集的本质概率分布,所以就需要一个函数来评估“距离”,也就是 f 散度这个体系
kl 散度是 f 散度的一种形式,使用 f 散度的 GAN 也常被叫做 f-GAN,这种模式下,判别器的训练更接近于逼近散度,再去指导生成器的学习
最早的 js 散度,会有梯度消失的问题产生
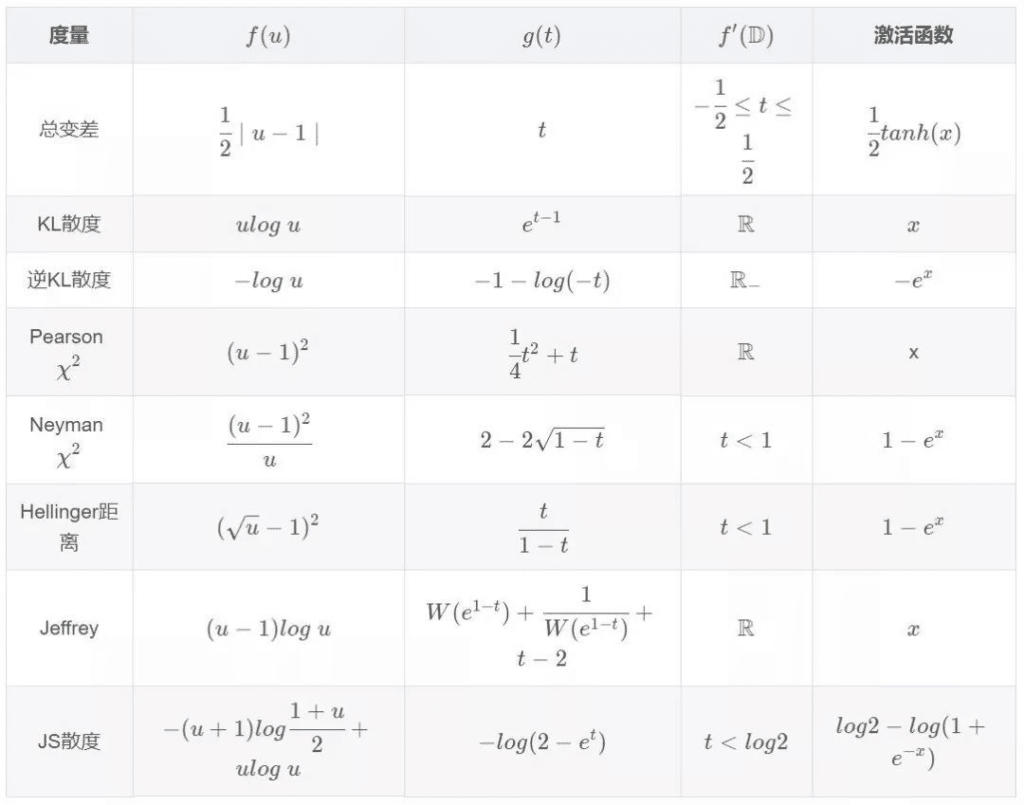
下图是 f 散度的各个度量形式,其中包括相应的原凸函数 $f(u)$ 、共轭函数还有激活函数 $f(u) = \max\limits _{t\notin f^{‘}(D)} \{tu – g(t)\}$ 这里就有点超出理解范围了,我看到的是共轭函数可以将任何函数化为凸函数,所以可以将 f 散度转变成可以计算的形式 然后就是 $t$ 的定义域为 $f(u)$ 的一阶导数的值域,对任意给定的u,遍历所有可能的t代入计算,然后寻找最大值