查找 – 数据结构

知识点

• 查找表
• 动态查找表
• 关键字
• 主关键字 次关键字
• ASL 平均搜索长度
• 哨兵
• 判定树 $ASL = \dfrac {{每层内节点数} \times {深度}} {内节点数}$
• 折半查找 递归 & while
• 内节点 外节点(叶子)
• 二叉排序树
• 平衡二叉树
• 阶 几叉
• 冲突 不同关键字映射到同一个地址
• 同义词 具有相同哈希散列函数值的两个关键字

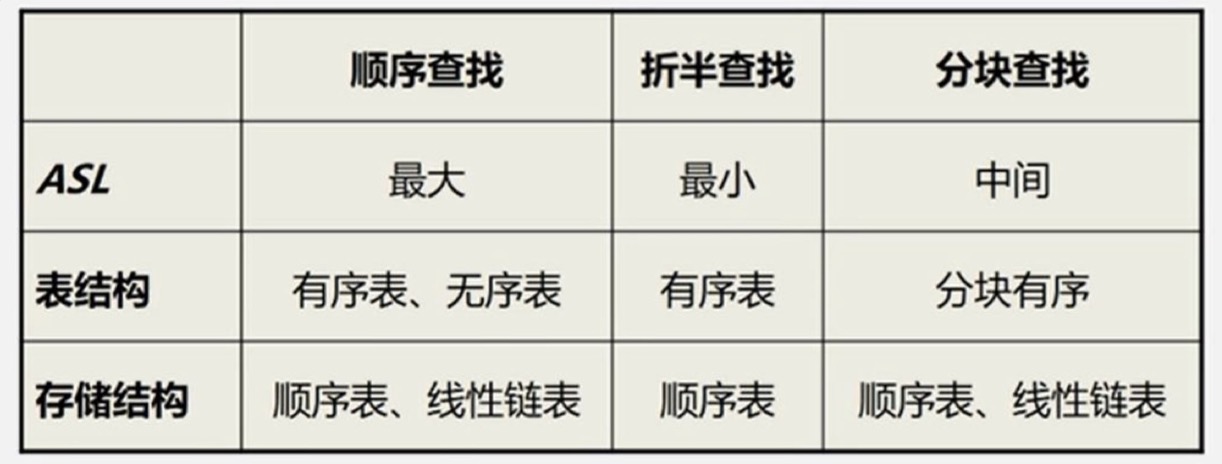
线性表查找

顺序查找

• 用哨兵减小不成功时ASL → 将比较写入 for 循环的条件中 i=length; 比较式; i- –
• 非等概率查找时，可按照查找概率进行排序

折半查找

• 判定树 ASL = 每层数量x层数/节点数
• n较大时 $ASL = \log2(n+1)-1$
• 适合顺序 不适合链式
• $ASL = {\frac {1} {n}}\sum^h_{j=1} j \cdot 2^{j-1} = \frac{n+1}{n}log_2(n+1)-1$
• while 的条件 low ≤ high

分块查找

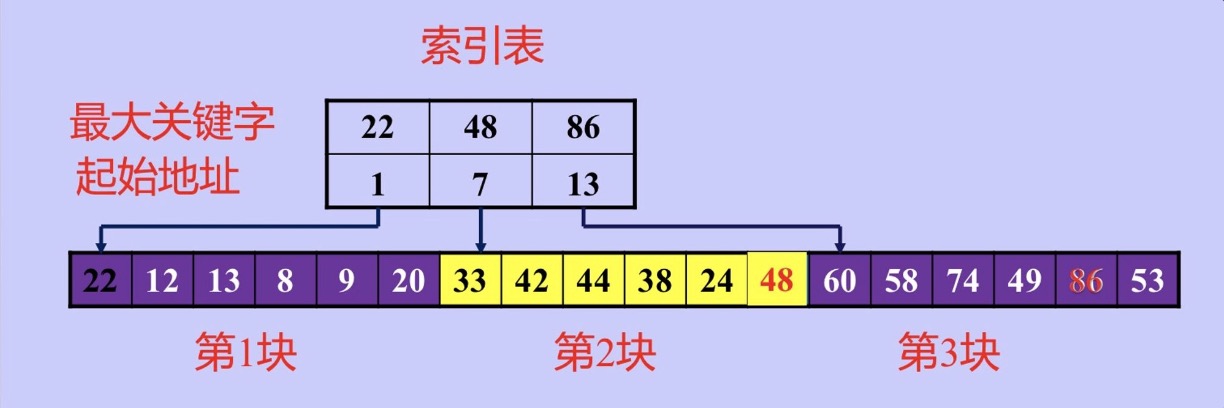
• 块内无序 块间有序
• 头指针构成索引表
• 先折半查找 再顺序查找

树表查找

二叉排序树 BST

• 中序遍历为递增序列 左根右依次递增
• 插入的元素一定在叶子上
• 生成 不同次序 → 不同形态
• 删除后重新接上即可 注意大小关系 检查中序序列
• ASL
  • 最好情况 —— 二分
  • 最坏情况 —— 顺序

平衡二叉树 AVL Tree

• 均衡 ⇒ 查找效率提高
• 平衡因子 = 左 – 右 应该 ≤ 1
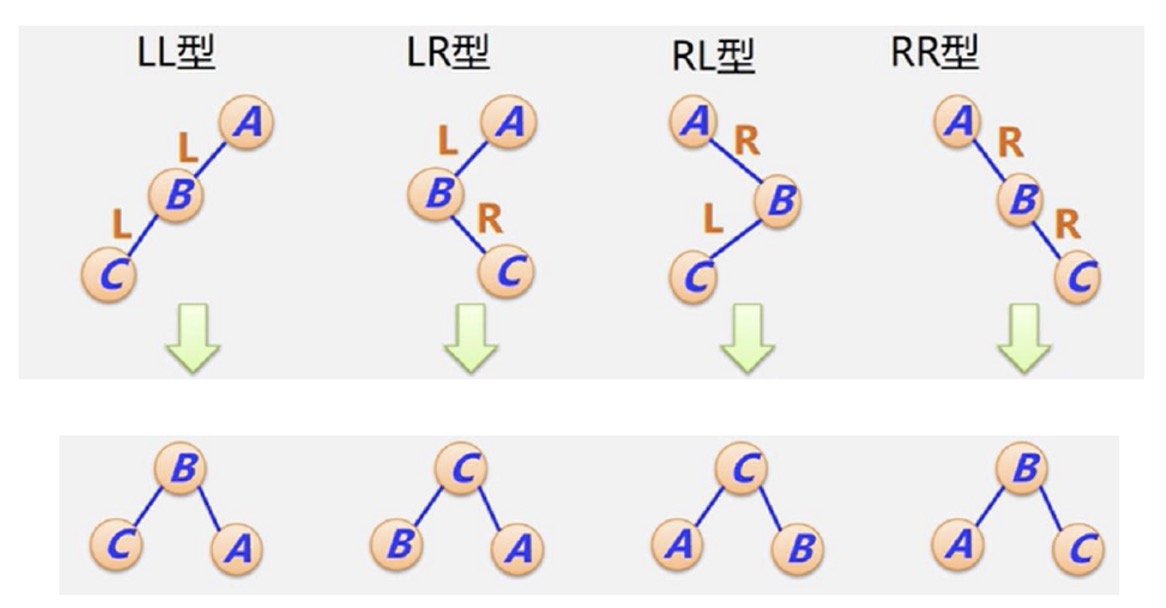
• 调整
  • 纯的 LL & RR 直接折
  • 混的 LR & RL 下面的穿上来
  • 保证中序序列不变 & 降低高度
  • 观察子树是否满足要求
  

B树

• 平衡 有序 多路 动态
• 磁盘管理等
• B树的平衡：叶子节点都在同一层
• 有序：每个节点的关键字有序
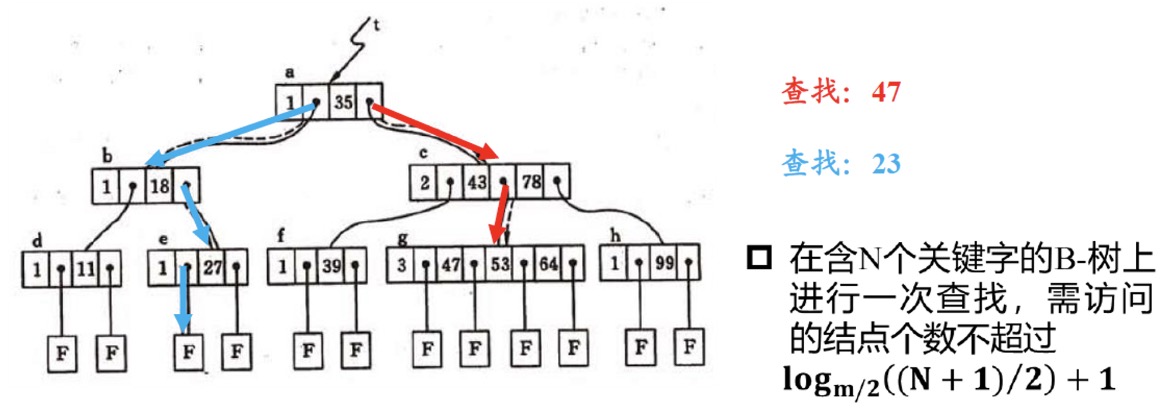
• m阶 ⇒ 至多m个子树 2-m
• 查找过程

散列表查找

• 函数关系直接算 O(1)
• 任意关键字的散列函数值要在表长范围内
• 原则：冲突尽可能少 & 解决方法
• 装填因子
  

• 查找效率
• ASL和散列函数 处理冲突方法 装填因子有关

构造方法：

• 直接定址 线性 ⇒ 不冲突但空间效率低
• 数字分析 事先知道关键字 & 位数大于地址位数
• 平方取中 平方后取中间几位 不知道全部关键字
• 折叠 叠加后几位 位数多且均匀
• 除留余数
  • $H(key) = key \mod {p}$
  • p 选小于表长的最大质数

处理冲突方法

• 开放地址法
  • 遇冲突去找下一个
  • 线性探测 ⇒ “聚集”
  • 二次探测
  • 伪随机探测
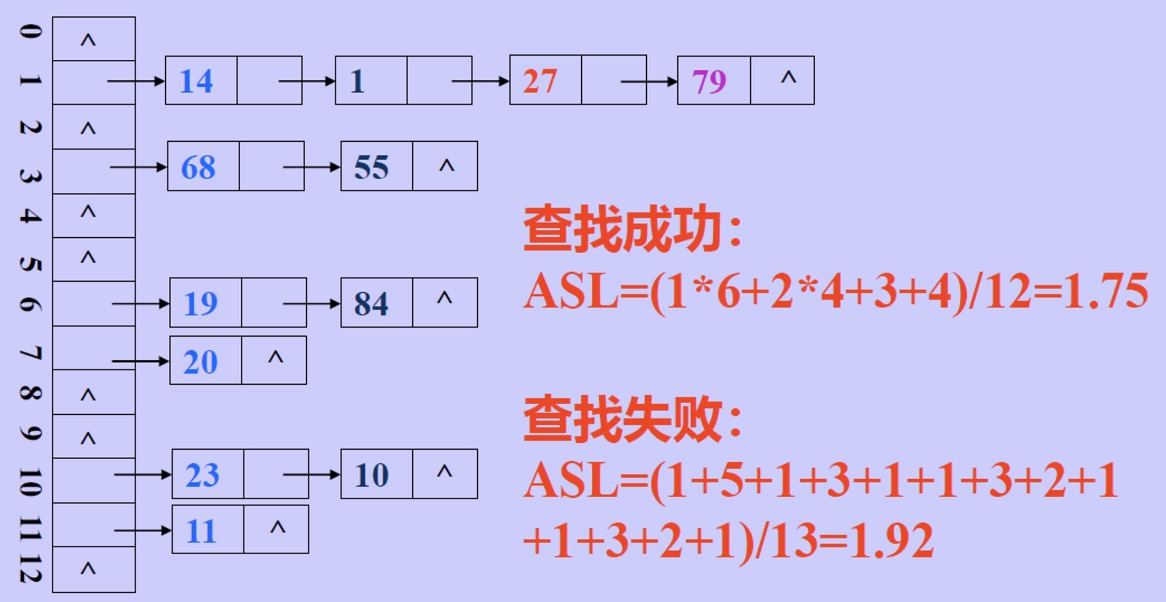
• 链地址法
  • 适用于不确定情况
• 失败时次数要比成功时次数多1 最后比1次空
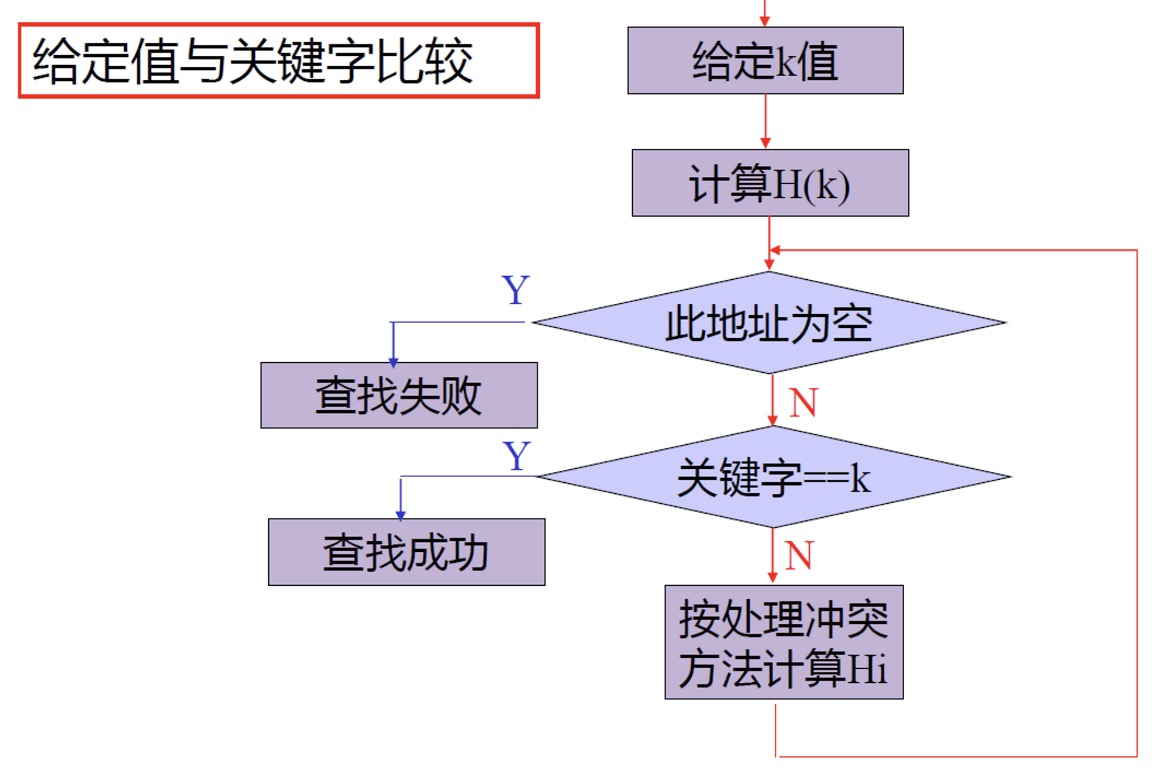
• 查找

Tips

• 涉及到画二叉排序树的过程 生成过程 删除操作等等 检查中序序列
• 调整失衡二叉树 别硬套 做完第一步 不行就瞪
• 根据序列生成平衡二叉树 看清楚什么时候需要调整 不要在没问题的时候调整
• 判断题 & 概念题 考虑空树
• 折半查找 需要考虑多个连续重复数字 导致二分时取不到第一个 解决方法如下程序：

int Search_Bin(SSTable ST, int key){
    int begin = 1,last = ST.length;
    int left = -1;
    while(begin<=last){
        int mid = (begin+last)/2;
        if(key==ST.R[mid].key){
            left = mid;
            while(1) {
                --left;
                if(ST.R[left].key != key) return left+1;
            }
        }else if(key<ST.R[mid].key){
            last = mid-1;
        }else if(key>ST.R[mid].key){
            begin = mid+1;
        }
    }
    return -1;
}

程序实现

//
// Created by XFishalways on 2022/12/13.
//
​
/**
 * 折半查找
 */
​
# include <stdio.h>
#include <stdlib.h>
​
typedef struct {
    int key;
}ElemType;
typedef  struct
{
    ElemType *R;
    int  length;
} SSTable;
​
int Search_Bin(SSTable ST, int key);
​
int main() {
    SSTable S;
    int x;
    scanf("%d %d", &S.length, &x);
    S.R = (ElemType*) malloc((S.length + 1) * sizeof(ElemType));
    int i;
    for(i=1; i <= S.length; i++){
        scanf("%d",&S.R[i].key);
    }
    int key;
    for (int j = 0; j < x; j++) {
        scanf("%d",&key);
        int pos = Search_Bin(S, key);
        printf("%d", pos);
        if(j != x-1) printf("\n");
    }
    return 0;
}
int Search_Bin(SSTable ST, int key){
    int begin = 1,last = ST.length;
    int left = -1;
    while(begin<=last){
        int mid = (begin+last)/2;
        if(key==ST.R[mid].key){
            left = mid;
            while(1) {
                --left;
                if(ST.R[left].key != key) return left+1;
            }
        }else if(key<ST.R[mid].key){
            last = mid-1;
        }else if(key>ST.R[mid].key){
            begin = mid+1;
        }
    }
    return -1;
}