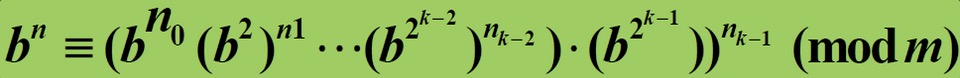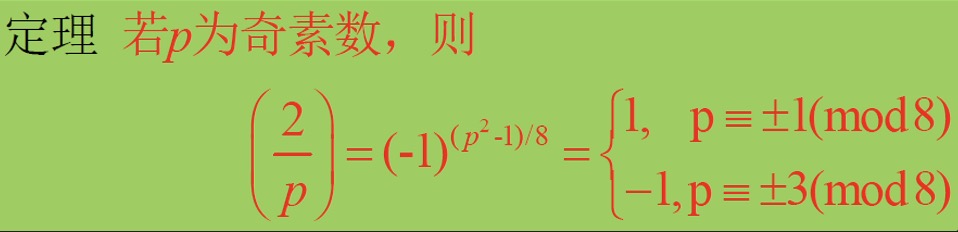同余
- 同余
- 等价关系(自反 对称 传递)
- 加减乘
- 互素的可以消去
- 关于模的因子 最小公倍数 同余
- 去九法
- 各位数字相加 & 基本运算规则
- 左右模九数相等
- 不一定能保证
- 剩余 剩余类 完全剩余系 简化剩余系(缩系)
- x, ax, ax+b 遍历一个完全剩余系
- 连续
- 互素 ⇒ 简化剩余类 简化剩余系
- x, ax 遍历一个简化剩余系
- Fermat小定理
- $a^{p-1} \equiv 1 \mod p or a^p \equiv a \mod p$
- p 素数
- x, y 分别遍历 p, q 的完全(简化)剩余系时,py + qx 遍历 pq 的完全(简化)剩余系
- 欧拉函数$ \psi (m)$
- 0-m互素个数 ⇒ 简化剩余系个数
- $s\sum m \cdot (1- \dfrac {1} {质因数})$
- $\psi(a^n) = a^n – a^{n-1}$
- 逆元 $a^{-1} \mod m$
- 充要条件 $(a, m) = 1 ⇒ 唯一一组 sa + tm =1 ⇒ a^{‘} = s$
- $aa^{‘} \equiv 1 \mod m$
- a → 可逆元
- $(p-1)! \equiv -1 \mod p$
- 欧拉定理 $a^{\psi (m)} \equiv 1 \mod m, (a, m) = 1$
- m n互素 ⇒ $\psi(mn) = \psi (m) \psi (n)$
- 算术基本定理 分解成素数乘积
同余式
$ax = b \mod m$
- 次数 deg f
- 解数 = (a, m)
- (a, m) = 1 时,唯一解 = $a^{‘} \mod m$
- 求解过程
- 判断(a, m) | b ? 有无解?
- 有解时 约分后 求 $ax \equiv 1 \mod m$ 的解 $x_0$
- 求原方程的解 $x_1$ ,直接乘就行
- 最后所有解为 $x_1 + \frac {m}{(a,m)} t \mod m$
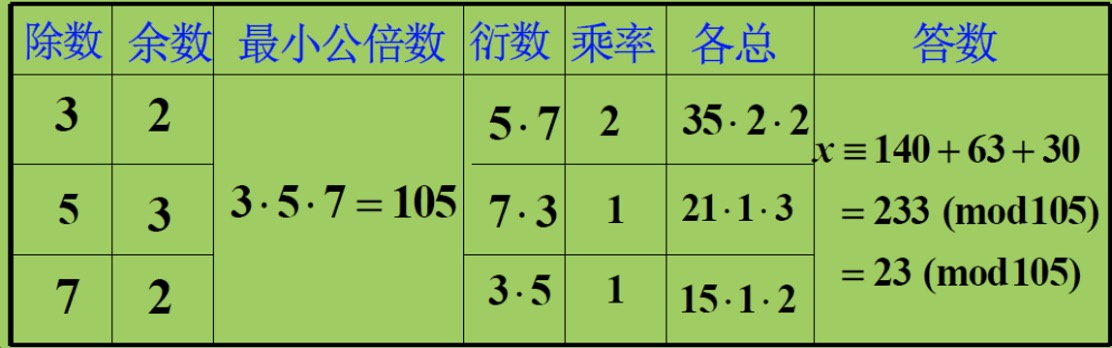
- 中国剩余定理
- 要 各个除数互素
- 具体计算:

- 乘率是衍数模除数的逆
- 可能需要先解单个方程 转为正确形式的方程组
- 还可以逐个求解然后带入下一个同余式
- 模重复平方计算法
- 求 $b^n \mod m$ 计算量大
- 将 n 写成二进制 $n = n_0 + n_12 + \cdot \cdot \cdot + n_{k-1}2^{k-1}$ ,n 取 0 或 1
- 则 计算可简化为

二次同余
$x^2 \equiv a \mod m$
其他形式可以通过配方 & 换元得到上面的
- m 的二次剩余 a:二次同余式有解
- 二次剩余数 = 非二次剩余数 = $\frac {p-1}{2}$ 个
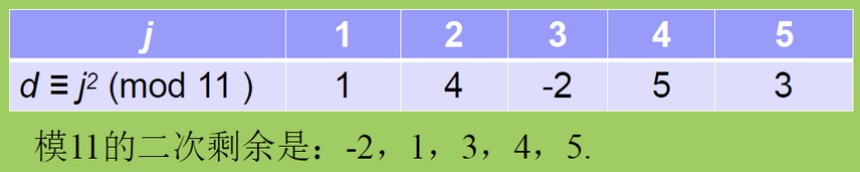
- 二次剩余求法
- 可直接试 1 → $\frac {p-1}{2}$ 的平方

- 欧拉判别法则 p是奇素数且互素
- 二次剩余 $a^{\frac {p-1}{2}} \equiv 1 \mod p$
- 二次非剩余 $a^{\frac {p-1}{2}} \equiv -1 \mod p$
- 可直接试 1 → $\frac {p-1}{2}$ 的平方
- a 是 m 二次剩余时,二次同余式有两个解
- 因为 1 和 -1 的性质
- 二次剩余 × 二次剩余 = 二次剩余
- 非 × 非 = 二次剩余
- 非 × 二次剩余 = 非
- -1 是二次剩余 $\Leftrightarrow p \equiv 1 \mod 4$
- 勒让德符号

- $(\frac {1}{p}) = 1, (\frac {-1}{p}) = (-1)^{\frac {p-1}{2}}$
- $(\frac {a+p}{p}) = (\frac{a}{p})$
- $(\frac{ab}{p}) = (\frac{a}{p})(\frac{b}{p})$ ⇒ 用于 a 的分解
- (a,p)=1 时,$(\frac{a^2}{p}) = 1$
- $(a, p) \not = 1$ 时,$(\frac{a}{p}) = 0$
- 计算
- -1 类直接算就行
- 2 类

- q 类 ⇒ 二次互反律 (\frac{q}{p}) = (-1)^{\frac{p-1}{2} \frac{q-1}{2}}(\frac{p}{q})
- 模 4 余 3 且有解时,解为 $\pm a^{\frac{p+1}{4}} \mod p$
- 其他

原根
- $ord_m(a)$
- 阶
- 原根 生成元 可以生成模 m 的群
- $ord_m(a) | d$ 从 $\psi(m)$ 的因子找原根
- 指数 $Ind_g(a)$,g原根,a余数

- 证明时 可通过欧拉判别法则 推原根 (二次非剩余)
- 原根存在的必要条件 2, 4, $p^{\alpha}, 2p^{\alpha}$
- $\psi(\psi(m))$ 个
- 判断原根

- 这样可以从因子里筛出1个原根 再用这个数的幂 也就是欧拉函数的那些个数的幂次 共 \psi(\psi(m)) 个


群
- <G, *>
- 左 右!!
- 概念们
- 代数系统 要求运算封闭 这是基础条件
- 半群 结合律
- 幺半群 有单位元
- 群 结合律 唯一单位元 & 逆元(相乘=单位元)
- Abel群 (交换群)
- 群有消去律
- Q \ {0} ⇒ Q – {0} ⇒ 非零有理数集
- Z / n Z ⇒ 模n的整数同余群 “循环” ⇒ 分n是否素数两种情况
- 交换群
- 子群 H ≤ G
- G本身是一个子群 平凡子群是一个子群
- 子群和原来的群 单位元 逆元相同
- $ab, a^{-1} \in H$
- $ab^{-1} \in H$
- 有限子集仅 $ab \in H$
- 平凡子群有两个:G 和 {e}
- $a^m = e$ 中最小正整数 m 为 a 的阶,|a| = m, 不存在 ⇒ 无限阶
- 加群中除单位元 所有元素都是无限阶
- 有限群中每个元素的阶都有限
- 循环群
- $\langle a \rangle = \{ a^n | n \in Z\}$ 这里的幂指做 n 次运算
- 循环群是 Abel 群
- $|G| = ord(a), G = \langle a \rangle$
- n 阶循环群有 $\psi(n)$ 个生成元
- 无限循环群有两个生成元 $a, a^{-1}$
- 子群也是循环群
- 阶的因子数量 = 子群数量
- 找生成元:将群的阶n分解
- 群也有 ≤ ≥ < >
- 2阶元生成的子群即为2 阶子群
- 陪集
- aH → H中每个元素和 a 做运算
- 求陪集 最后的集合要转换成 $x \in$ 群 的条件 写出代表元
- 左右写清楚 没事别化简
- a从群里面选 考虑全
- $a = ea \in aH$
- $a \in bH \to aH = bH$
- $ab^{-1} \in H \to aH = bH$
- 要么相等 要么不相交
- G = 所有 a 的 aH 并
- 陪集分解 左陪集代表系
- 以单位元为代表的陪集是子群
- 陪集中元素个数相等
- $aH \to Ha^{-1}$ 是双射
- 指数 [G:H]
- |G| = |H|[G:H]
- 子群的阶是群的阶的因子
- 对称群 $S_n$
- 和离散里的置换类似
- 从1开始 一个数表示一次交换 数对数 不是位置
- 运算就耐心一点看看哪些能消
- $|S_n| = n!$
- 正规子群
- 交换群的任意子群都是正规子群
- 群的阶 vs. 群内元素的阶
- G / H 表示正规子群 H 在 G 中的全部不同陪集的集合
- 剩余类群
- 商群
- G / H
- $aH \cdot bH = (ab)H$
- 单位元 H
- aH → 逆元 $a^{-1}H$
- G 模 H 的剩余类群
- 有限群 G 的商群 G / H 的阶是 G 的阶的因子
- 商群不是子群
- 同构
- 同态
- 同态双射 ⇒ 同构
- 自同构
- 证明:单射 + 满射 + 同态,反证同理
- 等价关系
- 群与双射变换群同构


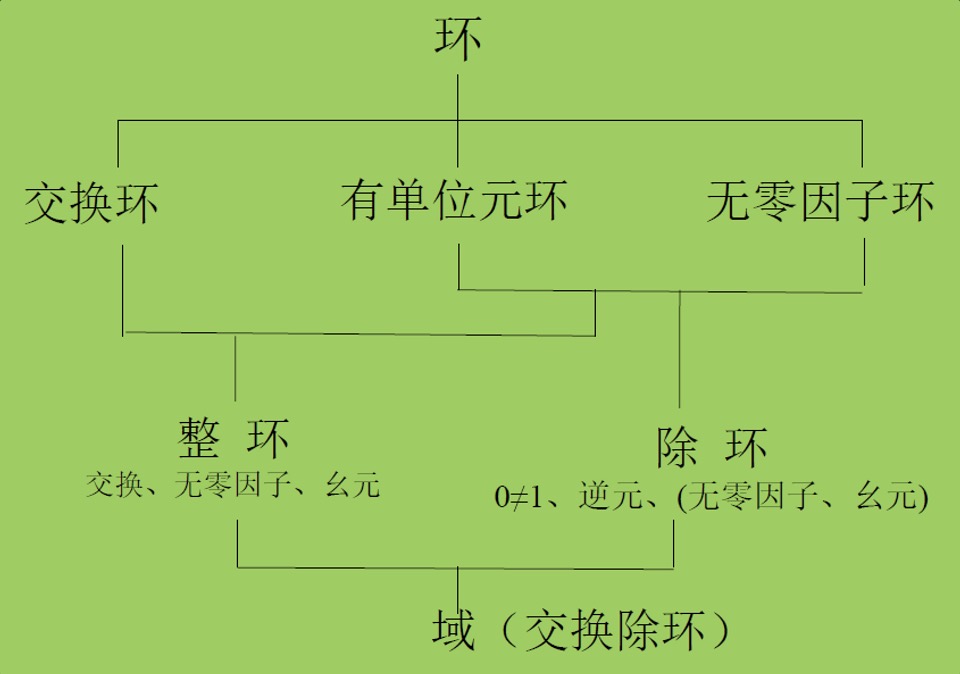
环
$<R, o_1, o_2>$
- 包含两种运算:加法 → 交换群,乘法 → 半群
- 分配律 左 & 右
- 不是所有环都有单位元
- 单位元唯一
- 数环
- 零因子 $a, b \implies a, b \not = 0, ab =0$
- 没有零因子 有消去律
- 整环 3个要求
- 交换环
- 单位元1
- 没有零因子
- 除环 3个要求
- 至少两个元
- 有单位元
- 非零元都有逆元
- ⇒ 无零因子
- 非零元 → 乘法群
- 域 交换除环
- 常写作 F
- 乘法满足交换律的除环
- 素数p 模p + & * 是一个域
- 域一定是整环
- 有限整环一定是域

- 无零因子环 R 中所有非零元的加法阶都相同
- char(R)
- 无零子环 R 的非零元的加法阶叫环R的特征 ⇒ 对任意 a \in R 都有 na = 0 的最小n
- 无限大 ⇒ char(R) = 0
- char(R) 存在则必为素数
- 整环、除环、域的特征是零或素数
- 特征为p ⇒ $(a+b)^p = a^p + b^p$
- 整环的特征是单位元“1”在加法群中的阶
- 整环加法群中非零元的阶 无穷 or 同一素数
- 子环 ⇒ $R^{’} 内 \forall a, b,要求 a – b, ab \in R^{‘}$
- 左理想 右理想 理想 ⇒ $\forall a \in R, \forall a^{‘} \in R^{‘}, aa^{‘} \in R^{‘}$
- 主理想
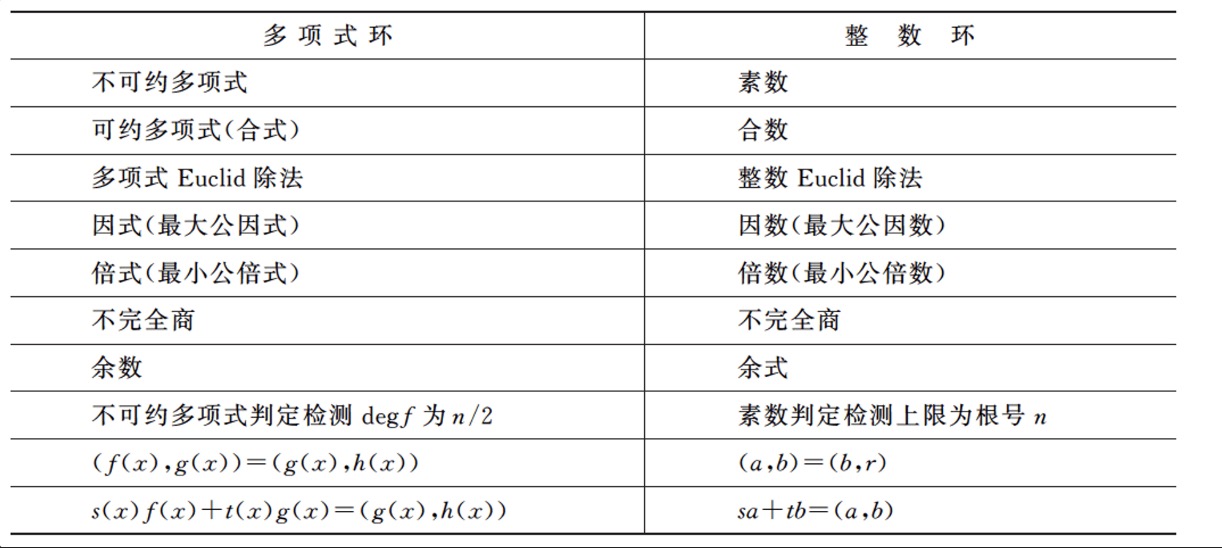
- 多项式环 R[x]
- 不可约
- 2阶 1次不可约 x+1, x,2次不可约 $x^2+x+1$:常数项为1,项数为奇
- $(f(x), g(x))$ 欧几里得除法的最后一个不完全商 就像整数那样 同样用欧几里得求多项式n
- 全体多项式的集合
- deg f 最高次数

- 可约多项式 不可约多项式 和所在环有关

- 多项式欧几里得除法 不完全商q(x) 余式r(x)
- $F_n$ 中对于 $\deg p \leq \frac{n}{2}$ 都不能整除 f(x) 则其不可约 如 $F_2$ 中有 x, x+1 两项不可约多项式
- 所有运算和实数的欧几里得除法类似 最大公因数 逆元等等
- 有限域 阶
- 阶 = $p^n$, 特征p
- 乘法运算是循环群 生成元为有限域的本原元(生成元)
- 有 $\psi(p-1)$ 个生成元
- 本原多项式
- $GF(2^n)$
- 有限域的构造
证明
同余
群
- 证 群等 概念
- 封闭
- 结合律
- 单位元
- 逆元
- 用结合律
- 把逆元乘过去
域
- 不可约多项式:次数n,用 n/2 及以下的不可约多项式除 有余式
Tips
- 判断题 小题 注意 非空 ……
- 群内如何运算 取决于群内的法则
- $a^0 = e$
- $a^{-n} = {a^{-1}}^n$
- 幂 就相当于 运算多少次
- 求解同余式组的步骤:
- 判断每个同余式是否有解,有一个无解,则组无解;
- 单个都有解时,判断模是否互素,互素则分别求解;不互素则分解为模的最大公因数和其他因数的同余式组(模互素了),计算模为公因数的同余式是否矛盾,矛盾则无解;不矛盾,如模还有公因数,继续分解和计算是否矛盾的过程,直至原同余式组通过分解模等价转化为模互素的同余式组求解;
- 解单个同余式,得到系数为1的解,如果有多个解,应分别联立同余式组,通过CRT得到多个解。
Show Comments